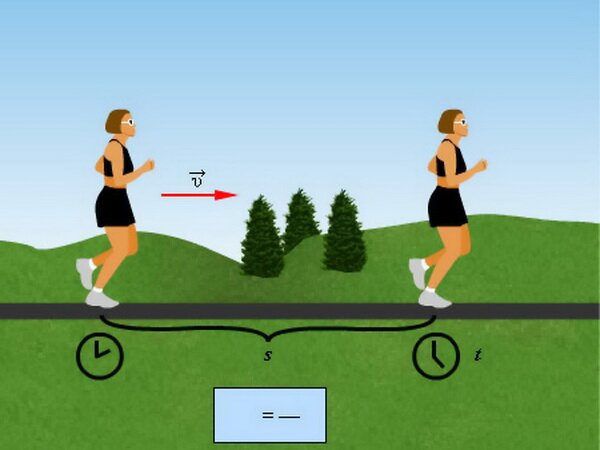
Равномерное движение – это движение с постоянной скоростью, то есть когда скорость не изменяется (v = const) и ускорения или замедления не происходит (а = 0).

Прямолинейное движение – это движение по прямой линии, то есть траектория прямолинейного движения – это прямая линия.

Равномерное прямолинейное движение – это движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения. Например, если мы разобьём какой-то временной интервал на отрезки по одной секунде, то при равномерном движении тело будет перемещаться на одинаковое расстояние за каждый из этих отрезков времени.

Скорость равномерного прямолинейного движения не зависит от времени и в каждой точке траектории направлена также, как и перемещение тела. То есть вектор перемещения совпадает по направлению с вектором скорости. При этом средняя скорость за любой промежуток времени равна мгновенной скорости:

v_cp = v

Скорость равномерного прямолинейного движения – это физическая векторная величина, равная отношению перемещения тела S за любой промежуток времени к значению этого промежутка t:

V = S  / t

Таким образом, скорость равномерного прямолинейного движения показывает, какое перемещение совершает материальная точка за единицу времени.

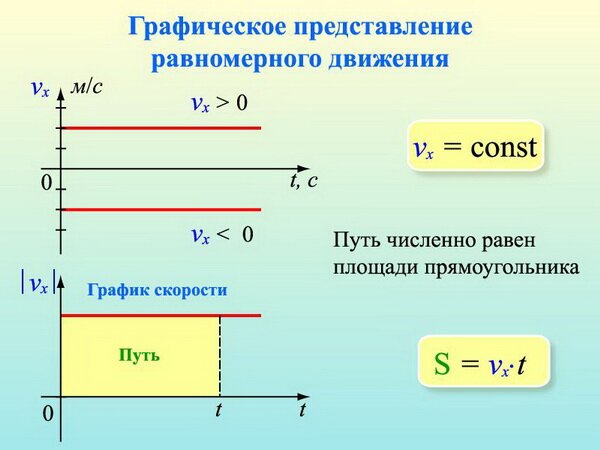
Перемещение при равномерном прямолинейном движении определяется формулой:

S = V  • t

Пройденный путь при прямолинейном движении равен модулю перемещения. Если положительное направление оси ОХ совпадает с направлением движения, то проекция скорости на ось ОХ равна величине скорости и положительна:

v_x = v,        то есть v > 0

Проекция перемещения на ось ОХ равна:

s = vt = x – x₀

где x₀ – начальная координата тела, х – конечная координата тела (или координата тела в любой момент времени)

Уравнение движения, то есть зависимость координаты тела от времени х = х(t), принимает вид:

х = x₀ + vt

Если положительное направление оси ОХ противоположно направлению движения тела, то проекция скорости тела на ось ОХ отрицательна, скорость меньше нуля (v < 0), и тогда уравнение движения принимает вид:

х = x₀ – vt

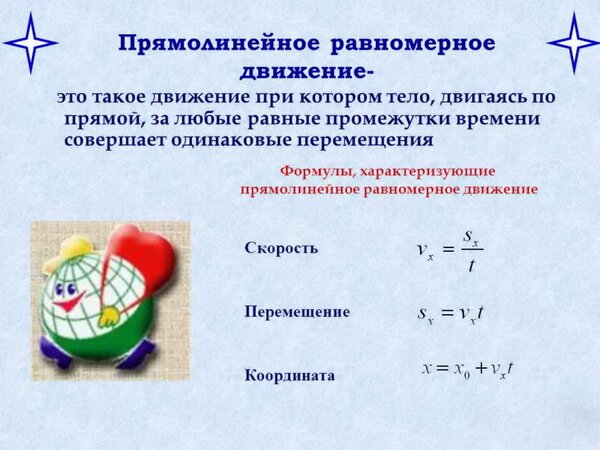
Приведенные формулы позволяют ответить на все вопросы, касающиеся равномерного движения.

Всякие измерения, и в частности измерения пути и промежутков времени, необходимые для нахождения скорости данного движения, всегда производятся не абсолютно точно, а лишь с некоторой определенной степенью точности. Поэтому, даже если измерения дают одну и ту же скорость движения на разных участках траектории, можно утверждать, что оно равномерно лишь с той степенью точности, с которой производились измерения.

Например, если определять время прохождения поезда между двумя километровыми столбами по минутной стрелке часов, то зачастую окажется, что на многокилометровом участке пути это время одно и то же: при этой степени точности движение поезда равномерно. Но если пользоваться секундомером и отсчитывать промежутки времени с точностью до долей секунды, то мы могли бы обнаружить, что эти промежутки времени не точно одинаковы, и, значит, движение поезда не является равномерным с этой, более высокой, степенью точности.